This document is not only an introduction to Clustering, but it also contains details on the Clustering Algorithms that Datagran offers, as well as the output tables. Hope you enjoy it.

Unsupervised Techniques

1. No labels are given to the learning algorithm, leaving it on its own to find structure in its input. Unsupervised learning can be a goal in itself (discovering hidden patterns in data) or a means towards an end (feature learning).

Unlabeled data: We have the input features X, but we do not have the labels Y.

The goal in such unsupervised learning problems may be to discover groups of similar examples within the data or to determine how the data is distributed in the space.

Clustering

Clustering can be considered the most important unsupervised learning problem; so, as with every other problem of this kind, it deals with finding a structure in a collection of unlabeled data.

It is the task of identifying similar instances and assigning them to clusters, or groups of similar instances.

‍

Clustering Applications

Customer Segmentation

You can cluster your customers based on purchases and activity in your website.

This is useful to understand who your customers are and what they need.

Semi-supervised learning

If you only have a few labels, you could perform clustering and propagate the labels to all instances in the same cluster.This is useful to increase the number of labels available for subsequent supervised algorithms and thus improve its performance.

Anomaly Detection

Any instance that has low affinity to all clusters is likely to be an anomaly.If you have clustered the users of your website based on their behavior, you can detect users with unusual behavior, such as an unusual number of request per second.This is useful in detecting defects in manufacturing, or fraud detection.

Clustering Algorithms

K Means

k-means is one of the most commonly used clustering algorithms that clusters the data points into a predefined number of clusters

Exclusive Clustering

Bisecting k-means

Bisecting k-means is a kind of hierarchical clustering using a divisive (or “top-down”) approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.Bisecting K-means can often be much faster than regular K-means, but it will generally produce a different clustering

Hierarchical Clustering

Gaussian Mixture Model (GMM)

A Gaussian Mixture Model represents a composite distribution whereby points are drawn from one of k Gaussian sub-distributions, each with its own probability

Probabilistic Clustering

Clustering flow

Main process flow

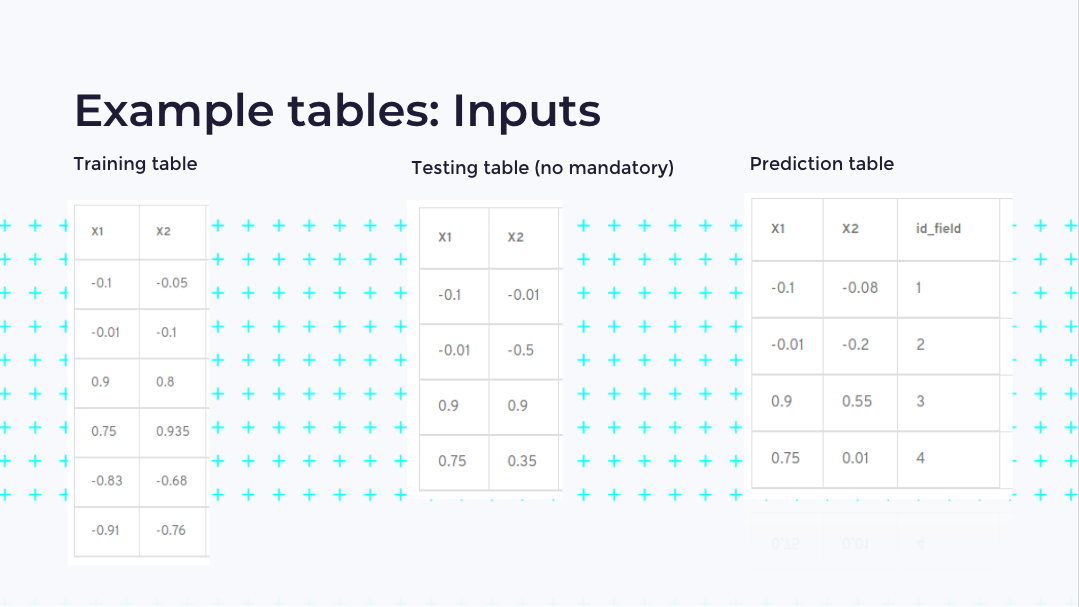
1. Define for each column, where its values must be of numeric type, the number of parameters is defined by you as needed, for this, 70-80% of the data can be randomly extracted.
2. Define the test table, this is defined with how the model is going to be tested, the same parameters or columns must be used as in the training data set, for this, 20 to 30% of the data can be randomly extracted. For total data, this table is not required.
3. K parameter, the procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori. The main idea is to define k centers, one for each cluster. These centroids should be placed in a smart way because of different location causes a different result. So, the better choice is to place them as much as possible far away from each other.
4. Define prediction table, here are the data to which you want to predict which cluster it belongs to, for this, you need the same input parameters in which the model was trained, plus an ID column to identify each set.

You can perform your model

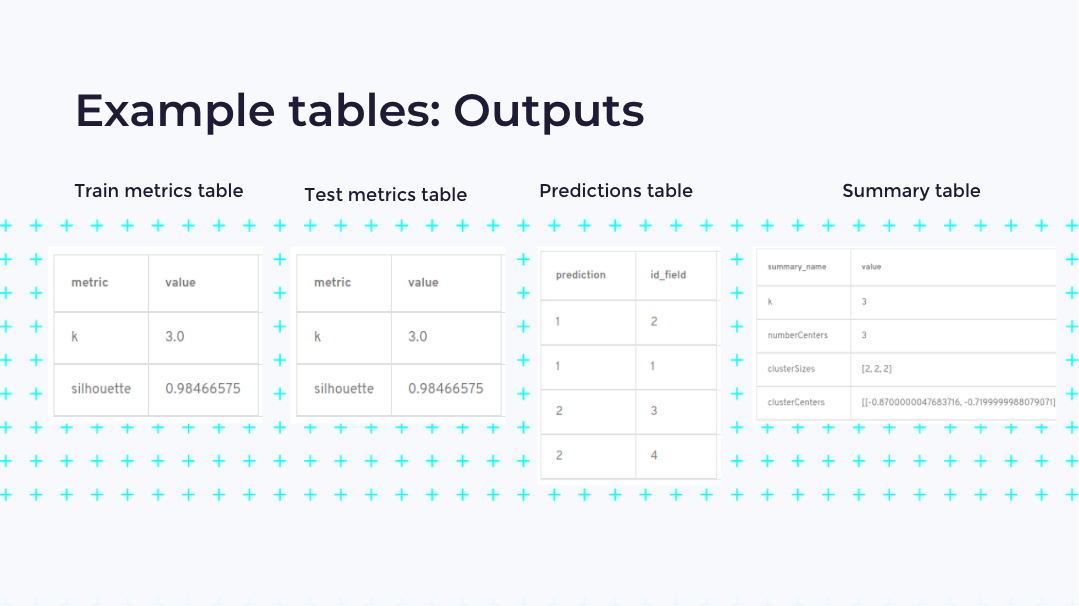
For each model you can modify its hyperparameters, thus edit the performance, each algorithm has its hyperparameters.

The most frequent are:

• k
• tol
• maxlter
• seed
• aggregationDepth
• weightCol
• distanceMeasure
• initSteps

‍